Jump to content

Applied mathematics

From Wikipedia, the free encyclopedia
For the company, see Applied Maths.
Efficient solutions to the vehicle routing problemrequire tools from combinatorial optimizationand integer programming.

Applied mathematicsis the application ofmathematical methodsby different fields such asphysics,engineering,medicine,biology,finance,business,computer science, andindustry. Thus, applied mathematics is a combination ofmathematical scienceand specialized knowledge. The term "applied mathematics" also describes theprofessional specialtyin which mathematicians work on practical problems by formulating and studyingmathematical models.

In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study inpure mathematicswhere abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics.

History

[edit]
A numerical solution to the heat equationon a pump casing model using the finite element method.

Historically, applied mathematics consisted principally ofapplied analysis, most notablydifferential equations;approximation theory(broadly construed, to includerepresentations,asymptoticmethods,variational methods, andnumerical analysis); and appliedprobability. These areas of mathematics related directly to the development ofNewtonian physics, and in fact, the distinction between mathematicians and physicists was not sharply drawn before the mid-19th century. This history left a pedagogical legacy in the United States: until the early 20th century, subjects such asclassical mechanicswere often taught in applied mathematics departments at American universities rather than inphysicsdepartments, andfluid mechanicsmay still be taught in applied mathematics departments.[1]Engineeringandcomputer sciencedepartments have traditionally made use of applied mathematics.

As time passed, Applied Mathematics grew alongside the advancement of science and technology. With the advent of modern times, the application of mathematics in fields such as science, economics, technology, and more became deeper and more timely. The development of computers and other technologies enabled a more detailed study and application of mathematical concepts in various fields.

Today, Applied Mathematics continues to be crucial for societal and technological advancement. It guides the development of new technologies, economic progress, and addresses challenges in various scientific fields and industries. The history of Applied Mathematics continually demonstrates the importance of mathematics in human progress.

Divisions

[edit]
Fluid mechanicsis often considered a branch of applied mathematics and mechanical engineering.

Today, the term "applied mathematics" is used in a broader sense. It includes the classical areas noted above as well as other areas that have become increasingly important in applications. Even fields such asnumber theorythat are part ofpure mathematicsare now important in applications (such ascryptography), though they are not generally considered to be part of the field of applied mathematicsper se.

There is no consensus as to what the various branches of applied mathematics are. Such categorizations are made difficult by the way mathematics and science change over time, and also by the way universities organize departments, courses, and degrees.

Many mathematicians distinguish between "applied mathematics", which is concerned with mathematical methods, and the "applications of mathematics" within science and engineering. Abiologistusing apopulation modeland applying known mathematics would not bedoingapplied mathematics, but ratherusingit; however, mathematical biologists have posed problems that have stimulated the growth of pure mathematics. Mathematicians such asPoincaréandArnolddeny the existence of "applied mathematics" and claim that there are only "applications of mathematics." Similarly, non-mathematicians blend applied mathematics and applications of mathematics. The use and development of mathematics to solve industrial problems is also called "industrial mathematics".[2]

The success of modern numerical mathematical methods and software has led to the emergence ofcomputational mathematics,computational science, andcomputational engineering, which usehigh-performance computingfor thesimulationof phenomena and the solution of problems in the sciences and engineering. These are often considered interdisciplinary.

Applicable mathematics

[edit]

Sometimes, the termapplicable mathematicsis used to distinguish between the traditional applied mathematics that developed alongside physics and the many areas of mathematics that are applicable to real-world problems today, although there is no consensus as to a precise definition.[3]

Mathematicians often distinguish between "applied mathematics" on the one hand, and the "applications of mathematics" or "applicable mathematics" both within and outside of science and engineering, on the other.[3]Some mathematicians emphasize the term applicable mathematics to separate or delineate the traditional applied areas from new applications arising from fields that were previously seen as pure mathematics.[4]For example, from this viewpoint, an ecologist or geographer using population models and applying known mathematics would not be doing applied, but rather applicable, mathematics. Even fields such as number theory that are part of pure mathematics are now important in applications (such ascryptography), though they are not generally considered to be part of the field of applied mathematicsper se. Such descriptions can lead toapplicable mathematicsbeing seen as a collection of mathematical methods such asreal analysis,linear algebra,mathematical modelling,optimisation,combinatorics,probabilityandstatistics, which are useful in areas outside traditional mathematics and not specific tomathematical physics.

Other authors prefer describingapplicable mathematicsas a union of "new" mathematical applications with the traditional fields of applied mathematics.[4][5][6]With this outlook, the terms applied mathematics and applicable mathematics are thus interchangeable.

Utility

[edit]
Mathematical financeis concerned with the modelling of financial markets.

Historically, mathematics was most important in thenatural sciencesandengineering. However, sinceWorld War II, fields outside the physical sciences have spawned the creation of new areas of mathematics, such asgame theoryandsocial choice theory, which grew out of economic considerations. Further, the utilization and development of mathematical methods expanded into other areas leading to the creation of new fields such asmathematical financeanddata science.

The advent of the computer has enabled new applications: studying and using the new computer technology itself (computer science) to study problems arising in other areas of science (computational science) as well as the mathematics of computation (for example,theoretical computer science,computer algebra,[7][8][9][10]numerical analysis[11][12][13][14]).Statisticsis probably the most widespreadmathematical scienceused in thesocial sciences.

Status in academic departments

[edit]

Academic institutions are not consistent in the way they group and label courses, programs, and degrees in applied mathematics. At some schools, there is a single mathematics department, whereas others have separate departments for Applied Mathematics and (Pure) Mathematics. It is very common for Statistics departments to be separated at schools with graduate programs, but many undergraduate-only institutions include statistics under the mathematics department.

Many applied mathematics programs (as opposed to departments) consist primarily of cross-listed courses and jointly appointed faculty in departments representing applications. Some Ph.D. programs in applied mathematics require little or no coursework outside mathematics, while others require substantial coursework in a specific area of application. In some respects this difference reflects the distinction between "application of mathematics" and "applied mathematics".

Some universities in theU.K. host departments ofApplied Mathematics and Theoretical Physics,[15][16][17]but it is now much less common to have separate departments of pure and applied mathematics. A notable exception to this is theDepartment of Applied Mathematics and Theoretical Physicsat theUniversity of Cambridge, housing theLucasian Professor of Mathematicswhose past holders includeIsaac Newton,Charles Babbage,James Lighthill,Paul Dirac, andStephen Hawking.

The Brown UniversityDivision of Applied Mathematics is the oldest applied math program in the U.S. [18] [19]

Schools with separate applied mathematics departments range fromBrown University, which has a large Division of Applied Mathematics that offers degrees through thedoctorate, toSanta Clara University, which offers only theM.S.in applied mathematics.[20]Research universities dividing their mathematics department into pure and applied sections includeMIT. Students in this program also learn another skill (computer science, engineering, physics, pure math, etc.) to supplement their applied math skills.

Associated mathematical sciences

[edit]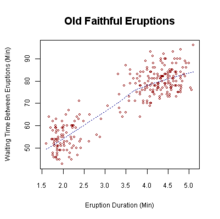
Applied mathematics has substantial overlap with statistics.

Applied mathematics is associated with the following mathematical sciences:

Engineering and technological engineering

[edit]

With applications ofapplied geometrytogether with applied chemistry.

Scientific computing

[edit]

Scientific computingincludes applied mathematics (especiallynumerical analysis[11][12][13][14][21]),computing science(especiallyhigh-performance computing[22][23]), and mathematical modelling in a scientific discipline.

Computer science

[edit]

Computer sciencerelies onlogic,algebra,discrete mathematicssuch asgraph theory,[24][25]andcombinatorics.

Operations research and management science

[edit]

Operations research[26]andmanagement scienceare often taught in faculties of engineering, business, and public policy.

Statistics

[edit]

Applied mathematics has substantial overlap with the discipline of statistics.Statistical theoristsstudy and improve statistical procedures with mathematics, and statistical research often raises mathematical questions. Statistical theory relies onprobabilityanddecision theory, and makes extensive use of scientific computing, analysis, andoptimization; for thedesign of experiments, statisticians usealgebraandcombinatorial design. Applied mathematicians andstatisticiansoften work in a department of mathematical sciences (particularly at colleges and small universities).

Actuarial science

[edit]

Actuarial scienceapplies probability, statistics, and economic theory to assess risk in insurance, finance and other industries and professions.[27]

Mathematical economics

[edit]

Mathematical economicsis the application of mathematical methods to represent theories and analyze problems in economics.[28][29][30]The applied methods usually refer to nontrivial mathematical techniques or approaches. Mathematical economics is based on statistics, probability, mathematical programming (as well as othercomputational methods), operations research, game theory, and some methods from mathematical analysis. In this regard, it resembles (but is distinct from)financial mathematics, another part of applied mathematics.[31]

According to theMathematics Subject Classification(MSC), mathematical economics falls into theApplied mathematics/otherclassification of category 91:

Game theory, economics, social and behavioral sciences

withMSC2010classifications for 'Game theory' at codes91AxxArchived2015-04-02 at theWayback Machineand for 'Mathematical economics' at codes91BxxArchived2015-04-02 at theWayback Machine.

Other disciplines

[edit]

The line between applied mathematics and specific areas of application is often blurred. Many universities teach mathematical and statistical courses outside the respective departments, in departments and areas includingbusiness,engineering,physics,chemistry,psychology,biology,computer science,scientific computation,information theory, andmathematical physics.

See also

[edit]

References

[edit]
  1. ^Stolz, M. (2002), "The History Of Applied Mathematics And The History Of Society",Synthese,133(1): 43–57,doi:10.1023/A:1020823608217,S2CID34271623
  2. ^University of Strathclyde (17 January 2008),Industrial Mathematics, archived fromthe originalon 2012-08-04, retrieved8 January2009
  3. ^abPerspectives on Mathematics Education: Papers Submitted by Members of the Bacomet Group, pgs 82-3.Editors: H. Christiansen, A.G. Howson, M. Otte. Volume 2 of Mathematics Education Library; Springer Science & Business Media, 2012.ISBN9400945043, 9789400945043.
  4. ^abSurvey of Applicable Mathematics, pg xvii (Foreword).K. Rektorys; 2nd edition, illustrated. Springer, 2013.ISBN9401583080, 9789401583084.
  5. ^THOUGHTS ON APPLIED MATHEMATICS.
  6. ^INTERNATIONAL CONFERENCE ON APPLICABLE MATHEMATICS (ICAM-2016).Archived2017-03-23 at theWayback MachineThe Department of Mathematics, Stella Maris College.
  7. ^Von Zur Gathen, J., & Gerhard, J. (2013). Modern computer algebra. Cambridge University Press.
  8. ^Geddes, K. O., Czapor, S. R., & Labahn, G. (1992). Algorithms for computer algebra. Springer Science & Business Media.
  9. ^Albrecht, R. (2012). Computer algebra: symbolic and algebraic computation (Vol. 4). Springer Science & Business Media.
  10. ^Mignotte, M. (2012). Mathematics for computer algebra. Springer Science & Business Media.
  11. ^abStoer, J., & Bulirsch, R. (2013). Introduction to numerical analysis. Springer Science & Business Media.
  12. ^abConte, S. D., & De Boor, C. (2017). Elementary numerical analysis: an algorithmic approach.Society for Industrial and Applied Mathematics.
  13. ^abGreenspan, D. (2018). Numerical Analysis. CRC Press.
  14. ^abLinz, P. (2019). Theoretical numerical analysis. Courier Dover Publications.
  15. ^For example see,The Tait Institute: History (2nd par.). Accessed Nov 2012.
  16. ^Dept of Applied Mathematics & Theoretical Physics.Queen's University, Belfast.
  17. ^DAMTP Belfast ResearchGate page.
  18. ^Suzuki, Jeff (2009-08-27).Mathematics in Historical Context. MAA. p. 374.ISBN978-0-88385-570-6.
  19. ^Greenberg, John L.; Goodstein, Judith R. (1983-12-23)."Theodore von Kármán and Applied Mathematics in America"(PDF).Science.222(4630): 1300–1304.Bibcode:1983Sci...222.1300G.doi:10.1126/science.222.4630.1300.PMID17773321.S2CID19738034.
  20. ^Santa Clara University Dept of Applied Mathematics, archived fromthe originalon 2011-05-04, retrieved2011-03-05
  21. ^Today, numerical analysis includesnumerical linear algebra,numerical integration, andvalidated numericsas subfields.
  22. ^Hager, G., & Wellein, G. (2010). Introduction to high performance computing for scientists and engineers. CRC Press.
  23. ^Geshi, M. (2019). The Art of High Performance Computing for Computational Science, Springer.
  24. ^West, D. B. (2001). Introduction to graph theory (Vol. 2). Upper Saddle River: Prentice Hall.
  25. ^Bondy, J. A., & Murty, U. S. R. (1976). Graph theory with applications (Vol. 290). London: Macmillan.
  26. ^Winston, W. L., & Goldberg, J. B. (2004). Operations research: applications and algorithms (Vol. 3). Belmont: Thomson Brooks/Cole.
  27. ^Boland, P. J. (2007). Statistical and probabilistic methods in actuarial science. CRC Press.
  28. ^Wainwright, K. (2005). Fundamental methods of mathematical economics/Alpha C. Chiang, Kevin Wainwright. Boston, Mass.: McGraw-Hill/Irwin,.
  29. ^Na, N. (2016). Mathematical economics. Springer.
  30. ^Lancaster, K. (2012). Mathematical economics. Courier Corporation.
  31. ^Roberts, A. J. (2009). Elementary calculus of financial mathematics (Vol. 15). SIAM.

Further reading

[edit]

Applicable mathematics

[edit]
[edit]
Wikiversity has learning resources about School:Mathematics
Wikibooks has a book on the topic of: Applicable Mathematics
Retrieved from " https://en.wikipedia.org/w/index.php?title=Applied_mathematics&oldid=1240045574"
Baidu
map